最近本人学习了一下伯克利的 EE247 课程中的滤波器相关的部分。在该课程中,提到了多种结构下的「品质因数(Q 值)」的定义,包括元器件、极点以及带通滤波器等等。同时在这之前,本人也曾学到过一些结构的 Q 值公式。但是在这些学习过程中,存在着一个一直不理解的点:为什么对于同一个被叫做「Q 值」的东西,在不同的情况下竟然有这么多种看似完全不相干的定义方式?这一个问题困扰了本人许久,也导致本人一直没能理解 Q 值的意义。
最近在接触了 EE247 课程后,这个困扰了许久的问题又重新浮现。为了彻底弄清楚这个问题,本人最近对各种结构的 Q 值的定义以及计算公式进行了一番思考和整理,以期能够找到这些 Q 值之间的联系。最终发现,这些 Q 值或多或少的都能够与「二阶系统的传递函数」扯上关系[1],也许这才是 「Q 值」本质上的意义。
1 各种典型结构的 Q 值
在讨论这些 Q 值之间的联系之前,本文首先整理一下各种典型结构的 Q 值计算公式,以便顺便为大家复习一下各种结构的 Q 值相关的定义以及计算方式。
1.1 非理想电感元器件
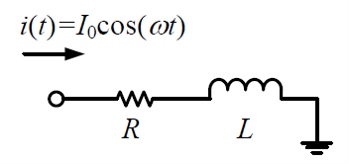
对于一个带有串联电阻的非理想的电感元器件,可以用电路图表示为:
对于一个非理想的电感元器件,它的 Q 值的定义方式为:
$$ Q=2\pi \frac{\text{每周期存储的最大能量}}{\text{每周期消耗的能量}} $$(如果假设这个电感元件只包含串联电阻这一个非理想特性,则)可以用来计算该电感元器件 Q 值的另一个公式为:
$$ Q=\frac{X(\omega )}{R(\omega )} $$由于使用上面这个公式来计算元器件的品质因数过于简洁好用,并且这个公式在大多数条件下都是成立的,因此很多情况下人们会将上面这个公式作为元器件 Q 值的定义公式,并使用该公式计算电感 Q 值。但是需要注意的是,这个公式并不是在任何条件下都成立的,下文中会提到这一点。
使用上述公式即可计算出带有等效串联电阻的电感的 Q 值为:
$$ Q=\frac{\omega L}{R} $$1.2 非理想电容元器件
这里假设非理想电容为带有一个等效串联电阻(ESR)的电容元器件,如下图:
同样通过上述 1.1 节中的两种定义方式,可以计算出该元器件的 Q 值为:
$$ Q=\frac{1}{\omega RC} $$1.3 RLC 串联谐振电路
一个 RLC 串联电路如下图所示:
当该电路发生谐振时,电感和电容产生的阻抗刚好抵消,电路阻抗呈现纯电阻,达到最小值。这个频率就被称为谐振频率。
该电路的阻抗表达式为:
$$ Z=R+sL+\frac{1}{sC} $$因此,通过在谐振时该阻抗表达式的虚部为零,即可以得出谐振频率为:
$$ \omega L=\frac{1}{\omega C},\,\omega _{\mathrm{n}}=\frac{1}{\sqrt{LC}} $$这时,该电路的 Q 值也可以使用能量的定义方式来计算。由于谐振时,能量在电感和电容上不停的交换,因此这时每周期系统存储的能量的最大值也等于每周期内电感或者电容储存能量的最大值。通过该定义最终可以计算得出:
$$ Q=\frac{\omega _{\mathrm{n}}L}{R}=\frac{1}{\omega _{\mathrm{n}}RC}=\frac{1}{R}\sqrt{\frac{L}{C}} $$而对于该电路,Q 值也同样可以用谐振时电感和电容上的电压与电源电压的比值来定义。通过简单的计算即可得出,在谐振时,电感和电容上的电压值为激励电压值的 Q 倍。
1.4 RLC 并联谐振电路
一个 RLC 并联谐振电路的电路图如下图所示:
该电路谐振时,电容的容纳与电感的感纳互相抵消,系统只剩下一个电导成分。
该电路的导纳值表达式为:
$$ Y=G+sC+\frac{1}{sL} $$通过在谐振时该导纳表达式的虚部为零,即可以得出谐振频率为:
$$ \omega _{\mathrm{n}}=\frac{1}{\sqrt{LC}} $$可以看出,该电路的谐振频率与串联谐振电路的谐振频率表达式完全相同。
通过能量定义的方式,同样可以求出该系统的 Q 值。当该系统谐振时,同样能量在电感和电容上不停交换,同样的方式可以推导出 Q 值为:
$$ Q=\frac{R}{\omega _{\mathrm{n}}L}=\omega _{\mathrm{n}}RC=R\sqrt{\frac{C}{L}} $$而对于该电路,Q 值也可以用谐振时流过电感和电容上的电流与激励电流的比值来定义。通过简单的计算即可得出,在谐振时,电感和电容上的电流值为激励电流值的 Q 倍。
1.5 带通滤波器
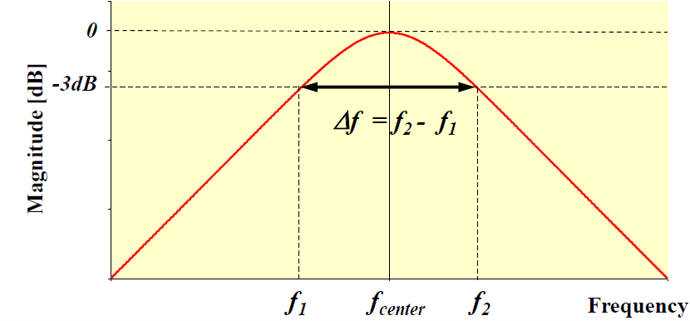
一个带通滤波器的频率特性如下图所示:
对于一个中心频率为 $f_{center}$,3 dB 带宽为 $f_2 – f_1$ 的带通滤波器而言,它的 Q 值定义为:
$$ Q=\frac{f_{\mathrm{center}}}{f_2-f_1} $$Q 值越大,说明该带通滤波器的通带范围越窄,选频特性越好。
1.6 (二阶)低通、高通滤波器
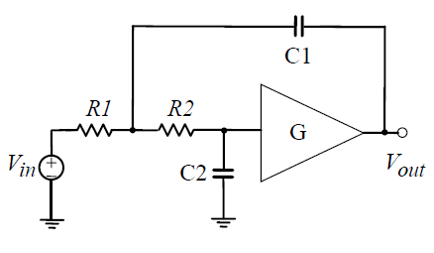
这里以二阶低通滤波器举例。对于一个如下图所示的二阶低通滤波器:
它的传递函数可以表示为:
$$ H(s)=\frac{G}{1+\frac{s}{\omega _{\mathrm{p}}Q}+\frac{s^2}{\omega _{\mathrm{p}}^{2}}} $$该传递函数中的「Q」,即为该低通滤波器的 Q 值,对于一个高通滤波器也类似。
对于上图所示的具体的电路,它的谐振频率 $\omega_p$ 和 Q 值表达式为:
$$ \omega _{\mathrm{p}}=\frac{1}{\sqrt{R_1C_1R_2C_2}},\,Q=\frac{\omega _{\mathrm{p}}}{\frac{1}{R_1C_1}+\frac{1}{R_2C_1}+\frac{1-G}{R_2C_2}} $$1.7 极点
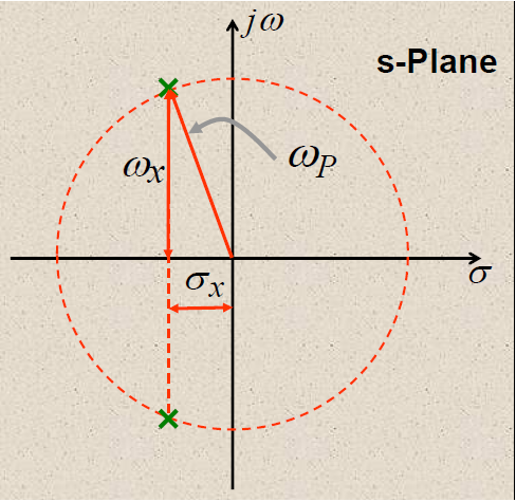
一对左半平面的共轭复极点如下图所示:
该极点的 Q 值定义为:
$$ Q=\frac{\omega _{\mathrm{p}}}{2\sigma _{\mathrm{x}}} $$2 二阶传递函数与 Q 值的关系
本人在思考这些 Q 值之间的联系时,偶然想起来自动控制原理中学过一个被称为「二阶系统」的东西。而对于一个标准的二阶低通滤波器,它的系统的传递函数,不就是一个二阶系统吗?当想到这一点时,本人忽然隐约的感觉到,可能所有的 Q 值的定义都能跟一个二阶系统扯上关系,而 Q 值的本质,就是自控中学习到的二阶系统的 $\zeta$ 参数(即阻尼系数)。
自控原理课程中常用的二阶系统的表达式为:
$$ G(s)=\frac{Y(s)}{U(s)}=\frac{{\omega _n}^2}{s^2+2\zeta \omega _ns+{\omega _n}^2} $$对于这个公式,可以对它进行一个变形。将分子和分母同时除以 $\omega _n$,即可得到表达式:
$$ G(s)=\frac{1}{\frac{s^2}{{\omega _n}^2}+\frac{2\zeta s}{\omega _n}+1} $$把它和一个标准的二阶低通滤波器的传递函数来比较一下:
$$ H(s)=\frac{1}{1+\frac{s}{\omega _{\mathrm{p}}Q}+\frac{s^2}{\omega _{\mathrm{p}}^{2}}} $$是不是发现很像?没错,这样对比就可以看出来,$\omega_{\mathrm{p}}$ 即为 $\omega_{\mathrm{n}}$,而 Q 即为:
$$ Q=\frac{1}{2\zeta} $$是不是好像明白了些啥?如果还不明白,那么本人接下来放两个图,看了这两个图,大家可能就会明白了。
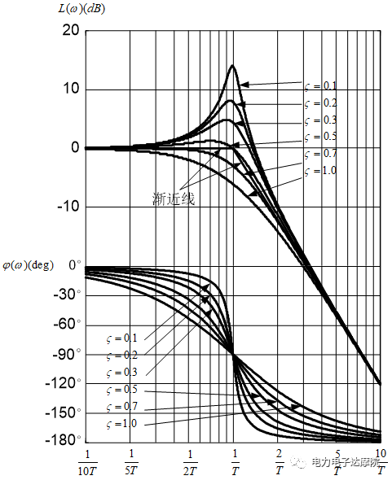
第一个图是对于一个自控中出现的二阶系统,它的幅频特性和 $\zeta$ 参数的关系:
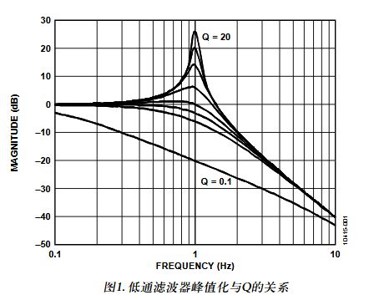
第二个图是对于一个标准的低通滤波器,它的幅频特性与 Q 值得关系:
两幅图是不是特别像?因此,本人猜想,某种意义上 Q 值只是二阶系统中的 $\zeta$ 参数的另一种表示方法罢了(二阶系统中的阻尼系数又是一个具有非常明确的物理意义的量,大家可以去《自动控制原理》、《信号与系统》以及《大学物理》等书籍上学习阻尼系数这个参数,或者去 b 站等视频平台观察二阶系统阻尼系数的试验和仿真视频,这里本人就不对其做过多介绍)。而对于其他的 Q 值的定义,因该也是可以找到一个相应的二阶系统来对应上的。下一节就来说明这一点。
3 各 Q 值对应的二阶传函
上文中提到的这些 RLC 电路,其实都是可以与一个二阶传递函数关联起来的。下面就来说明这个问题。就先从 RLC 谐振电路开始吧。
3.1 RLC 串联谐振电路
对于上文中提到的 RLC 串联谐振电路,如果考虑电阻上的电压值,就可以得到这样一个表达式:
$$ H_R(s)=\frac{R}{R+sL+\frac{1}{sC}}=\frac{sCR}{1+sCR+s^2LC} $$也许大家会发现这个表达式,这个表达式就是一个很典型的二阶传递函数形式。没错,因此根据这个表达式,就一定能计算出来一个 $\omega_{\mathrm{p}}$ 和一个 Q 值。
通过与上文中的带 Q 形式的二阶传递函数进行比较,就可以找出如下的对应关系:
$$ \frac{1}{\omega _{\mathrm{n}}^{2}}=LC, \frac{1}{\omega _{\mathrm{n}}Q}=CR $$通过这两个表达式,就可以求出上文中提到的该电路结构的 $\omega_{\mathrm{p}}$ 和 Q 值了。
由此,可以看出,RLC 串联谐振电路的 Q 值,是可以和一个二阶传递函数相关联的。
3.2 RLC 并联谐振电路
对于一个 RLC 并联谐振电路系统,流过它的电阻上的电流可以表示为:
$$ H_R(s)=\frac{\frac{1}{R}}{\frac{1}{R}+sC+\frac{1}{sL}}=\frac{\frac{sL}{R}}{1+\frac{sL}{R}+s^2LC} $$可以看出,这个表达式也是一个二阶传函的形式。
因此,与上文中带 Q 形式的二阶传函进行对比,同样可以找出一个对应关系:
$$ \frac{1}{\omega _{\mathrm{n}}^{2}}=LC,\,\frac{1}{\omega _{\mathrm{n}}Q}=\frac{L}{R} $$由此可以看出,并联 RLC 谐振电路的 Q 值,同样是可以与一个二阶传函相关联的。
3.3 (二阶)带通滤波器
由于一个高阶的滤波器可以由一阶滤波器和二阶滤波器组成,因此滤波器部分这里只讨论二阶滤波器的 Q 值。
对于一个二阶带通滤波器,一个比较好的例子即为上文中 RLC 串联电路中 R 的电压表达式:
$$ H_R(\omega )=\frac{R}{R+\mathrm{j}\left( \omega L-\frac{1}{\omega C} \right)} $$可以看出该表达式即为一个带通形式的表达式。对于该表达式,令 $η=ω/ω_0$,即可将该表达式变形为:
$$ H_R(\eta )=\frac{1}{1+\mathrm{j}Q(\eta -\frac{1}{\eta})} $$式中 Q 即为 RLC 串联谐振电路的 Q 值。令该表达式的值等于 $\frac{1}{\sqrt{2}}$,即可求出该带通滤波器的 3 dB 频率点。此时可以得出 $Q(\eta -\frac{1}{\eta})=\pm 1$,并最终可以解得:
$$ \eta _1=-\frac{1}{2Q}+\sqrt{(\frac{1}{2Q})^2+1},\,\eta _2=\frac{1}{2Q}+\sqrt{(\frac{1}{2Q})^2+1} $$ $$ \eta _2-\eta _1=\frac{\omega _2}{\omega _0}-\frac{\omega _1}{\omega _0}=\frac{1}{Q} $$ $$ Q=\frac{\omega _0}{\omega _2-\omega _1} =\frac{f _{center}}{f _2-f _1} $$由此,可以看出,二阶带通滤波器的 Q 值,也是可以通过某种方式与二阶传函扯上关系的。或者说二阶带通滤波器的 Q 值来源就是该滤波器的二阶传函。
3.4 (二阶)低通、高通滤波器
同样是使用上文中的 RLC 串联谐振电路举例。对于该串联谐振电路,它的电感和电容上的电压分别为:
$$ H_L(s)=\frac{sL}{R+sL+\frac{1}{sC}}=\frac{s^2LC}{1+sCR+s^2LC} $$ $$ H_C(s)=\frac{\frac{1}{sC}}{R+sL+\frac{1}{sC}}=\frac{1}{1+sCR+s^2LC} $$可以看出,该滤波器的表达式同样是一个二阶传递函数的形式(然而二阶低通和高通滤波器的表达式本身就该是一个二阶传递函数啊,不然为啥叫做二阶?)。大家可以尝试计算一下,使用该表达式提取出的 $\omega_{\mathrm{p}}$ 和 Q 值,就是这个 RLC 串联谐振电路的 Q 值。
3.5 (一对共轭)极点
对于上文中提到的极点的 Q 值,同样可以和一个二阶传递函数相关联。通过自控原理的书籍可以知道,一个二阶传递函数具有两个极点,其中一种很重要的情况就是具有一对共轭的复极点。而一对共轭的复极点也可以对应一个二阶传递函数。因此,一对共轭复极点的 Q 值是一定可以对应上一个二阶传函的 Q 值的。
这里我们用一个标准的二阶传函表达式来举例:
$$ G(s)=\frac{Y(s)}{U(s)}=\frac{{\omega _n}^2}{s^2+2\zeta \omega _ns+{\omega _n}^2} $$该表达式的两个极点为:
$$ s=-\zeta \omega _n\pm \omega _n\sqrt{\zeta ^2-1} $$假设该极点为一对共轭的复极点,则可以得出[2]:
$$ \omega _p=\omega _n,\,\sigma _x=\zeta \omega _n $$进而可以计算出该极点的 Q 值为:
$$ Q=\frac{\omega _{\mathrm{p}}}{2\sigma _{\mathrm{x}}}=\frac{1}{2\zeta} $$而 $\frac{1}{2\zeta}$ 表达式正好又是这个二阶传函的 Q 值表达式。因此,极点的 Q 值得本质就是一个它相对应的二阶传函的 Q值。
3.6 元器件的 Q 值
对于元器件的 Q 值与二阶传函的对应关系,这里只讨论电感的 Q 值,电容的对应方法和电感差不多。参考书[3]中提到了一种方法:对于电感在某一个频率下的 Q,可以通过假设给这个电感并联上一个具有一定电容值的电容,进而使得该电路可以在这个频率下谐振来求得,如下图:
这是可以求出电感上的电流为:
$$ H_L(s)=\frac{\frac{1}{R+sL}}{sC+\frac{1}{R+sL}}=\frac{1}{1+sRC+s^2LC} $$该传函对应的 Q 值为:
$$ Q=\frac{\omega L}{R} $$可以看出,通过该方法就可以将电感元件的 Q 值与一个二阶传函联系在一起。
4 总结
通过该章的分析可以看出,这些常见结构的 Q 值,的确是或多或少的都可以与一个二阶的传递函数来扯上联系。关于 Q 值的维基百科是这样描述的:
这个描述中可以看出,Q 的来源为一个共振系统。而由于大部分共振系统都可以用一个二阶传递函数来描述,因此 Q 也就合理的与二阶传递函数扯上关系了。由此可以看出,可能能量的定义方式才是 Q 值最本质的定义方式。
5 后记:一种「有点问题」的 Q 值计算方式
前文中我们提到,对于一个元器件的 Q 值,可以用这种方式计算:
$$ Q=\frac{X(\omega )}{R(\omega )} $$这种方式由于计算简单且大部分的情况下计算值与实际值几乎一致,因此被广泛的应用到了各种元器件以及类元器件结构(比如积分器)的 Q 值的测量和计算中。
但是,实际上这种计算方式在某些情况下是会有问题的。例如考虑一个带有寄生电阻和寄生电容的实际电感。这个电感在某个输入信号频率下,会与其的自身电容发生「自谐振」。前面我们提到过,当发生谐振时,系统的阻抗(或者导纳)表达式的虚部为 0。这时在使用这种方式计算该电感的 Q 值,就会发现——该电感的 Q 值为 0!
这显然是不正确的。在发生自谐振时,系统仍然存储有能量,只不过能量在电感和电容上面不停的交换而已。因此,这个时候系统的 Q 值就不可能为 0。但是这个表达式却给出了一个 0 的结果。
因此,这个表达式在某些情况下计算出来的值的确是不正确的。对于一个可能会产生自谐振的元器件而言,越接近于其谐振状态,这个表达式计算出来的值越不准确。对于其更详细的论述,大家可以去看这本参考书:Radio Frequency Integrated Circuits and Systems 2nd – Hooman Darabi


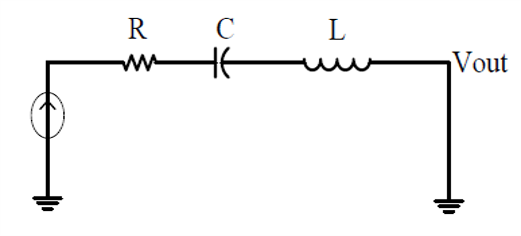


非常好的文章。我有幸和作者想到一起了,不过我们的路线恰好是反的。我是学自控原理时学到二阶系统,想起来模电里面的Q值,但是模电学的不扎实,已经忘了模电里Q怎么求的,于是赶紧上网来搜索。有幸搜到博主的文章,获益匪浅,感谢博主分享!
殊途同归哈哈。现在我做电路做的多了发现本科学习的那些看似用不到的课程实际上都对自己的领域或多或少的都有一些很重要的作用或者有一定的联系,只是当时实践太少导致自己完全没有发现,现在想起来当时没好好学真是悔之晚矣。
有幸看到这篇文章,对于没有学过自动控制原理的我也是受益匪浅的
文章里的公式都是tex语法有点不易阅读
这个可能是由于你的浏览器的问题,我这边试过火狐、edge 和 chrome 都不存在这个问题。
写的很清楚!感谢博主。
博主的文章很有帮助,是我看过相关的最成系列的文章。但是有一个小问题,关于非理想电容的等效回路,是否应该是电容和电阻并联,因为非理想电容存在漏电现象,这样的话电容Q的计算公式是否也有误呢。
对于你说的有漏电的非理想电容,可以等效为一个 C 和一个 R 的并联,那么在并联一个 L 的话,这样计算出来的 Q 的公式是一样的,只不过计算时电阻要取为并联。
或者你也可以使用能量的定义计算,就是使用每个周期存储的能量除以每个周期消耗的能量,这样算出来的 Q 肯定是没问题的。
请教博主一个问题:两个无源一阶RC滤波器级联(中间做buffer),得到的传输函数遵循二阶通式,由此得到的Q是0.5,但是二阶RC滤波器的Q值该如何定义(二阶RC滤波器不完全遵循二阶通式)?
你好,对于 Q 值这个东西,我的理解是只要有一个二阶多项式形式的分母,那么就可以根据这个分母来计算出一个 Q 来。只需要把分母画为二阶通式就可以了,就可以求出 Q 了。所以对与你说的这个二阶 RC 滤波器,我认为它的 Q 的定义就是分母多项式的 Q。