1 前言

一个单端的运算放大器通常会包含一个正输入端、一个负输入端和一个输出端。通常情况下，一个单端运放的输出端都是固定的，并且非常容易判断。但是在确定好输出端之后，对于运放的两个输入端，是不能按照自己的心情去随心所欲的标注的，而是需要对其进行判断，来确定哪个是正输入端哪个是负输入端。一旦正负输入端标错，就会造成运放外部电路由原来的负反馈变为正反馈，从而导致电路工作状态的异常。而对于全差分放大器，则存在正负输入端和正负输出端的判断为问题，如果判断失误同样会导致电路的工作异常。因此，正确判断运放的正负输入端是十分重要的。这里，本人将通过举例子的方式，来说明一下运放的正负输入端的判断方法。

2 需要了解的基本原理

2.1 叠加定理

通常当一个运放处于正常工作的情况下，它的两个输入端可以近似的看作被接在了两个理想的电压源上。而运放的电路结构通常较为复杂，同时对这两个输入来进行电路分析是十分困难的，因此在判断一个运放输入端的正负极性时，需要用到电路的叠加定理。电路的叠加定理可以表述为：「在线性电路中，当有多个电源作用时，任一支路电流或电压可看作由各个电源单独作用时在该支路中产生的电流或电压的代数和。当某一电源单独作用时，其它不作用的电源应置为零（电压源电压为零，电流源电流为零），即电压源用短路代替，电流源用开路代替。」

而对于运放电路，当它处于一个小信号工作模式时，即可将其看作一个线性电路。因此，电路的叠加定理0表明：在分析运放的某个输入端的正负极性时，可以将另一个输入端接到小信号地（电压源置 0），只对该输入端的极性进行分析，随后再使用同样的方式对另一个输入端进行分析，即可得出两个输入端的正负极性。

2.2 极性传递

由于运放通常工作在小信号模式下，因此在对运放的正负输入端进行分析时，通常是的分析方法为在运放的输入端施加一个极性为「㊉」的 AC 小信号，并根据该 AC 小信号传递到输出端的极性的正「㊉」负「㊀」来判断该输入端的正负极性。因此，在进行运放极性分析之前，需要先了解一下典型的极性传递情况。如果大家不了解什么是极性传递以及典型的极性传递情况，可以去看这篇文章：文章连接。

3 单端运放正负输入端分析

3.1 简单的五管 OTA

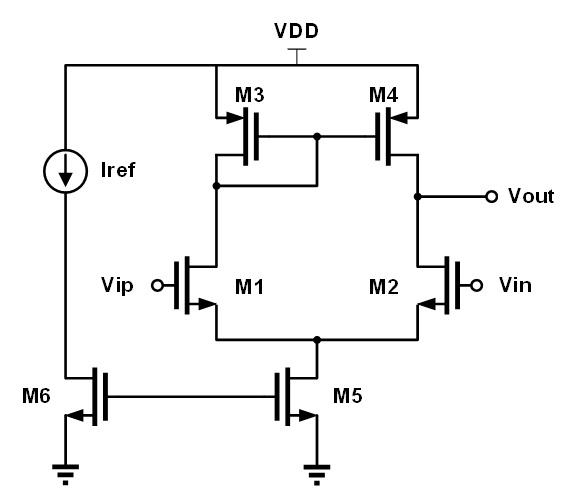
首先本人先从五管 OTA 这样一个非常简单的例子开始，来介绍运放正负输入端的判断方法。一个五管 OTA 的电路图如下图所示。五管 OTA 为单极运放结构，可以较为容易的使用环路极性法来进行分析。

接下来对该运放的输入端进行分析。这里首先分析运放右侧的输入端的正负。在对该输入端的正负极性进行分析时，首先需要先将运放的另一个输入端置零（在这个运放里面就是将其接到小信号地），并在该输入端出施加一个极性为「㊉」的交流小信号。

通过对该运放的原理图进行分析可以看出，该运放右侧的输入信号通过一个晶体管 M2，从 M2 的栅极传递到 M2 的漏极（即运放的输出），而根据晶体管的栅极和漏极的极性传递关系为反相的结论，则该输入传递到运放输出端的极性为「㊀」，因此该输入端为运放的反相输入端。

随后分析运放的左侧输入端，再分析该输入端时需要将运放的另一个输入端置零。该输入端首先经过了晶体管 M1，从 M1 的栅极传递到 M1 的漏极，极性反相，因此 M1 漏极处的极性为「㊀」； 随后该信号经过晶体管 M4，由晶体管 M4 的栅极传递到达输出端，极性反相，因此最终到达输出端的极性为「㊉」。由此该输入端为运放的正向输入端。

下图表示了该五管 OTA运放的两个输入端到输出端的极性传递过程。

3.2 Cascode 单极运放

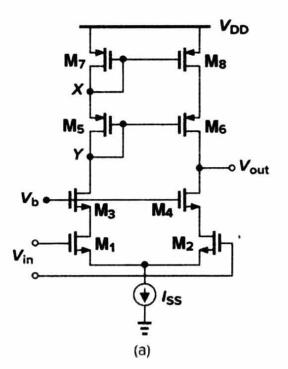
接下来分析一个稍微复杂一点的情况——单极的 Cascode 运放。单极的 Cascode 运放的电路原理图如下图所示。该运放相比于普通的五管 OTA 运放，增加了两个晶体管，因此分析的难度有所提升，但是同样可以使用极性传递的方式进行分析。

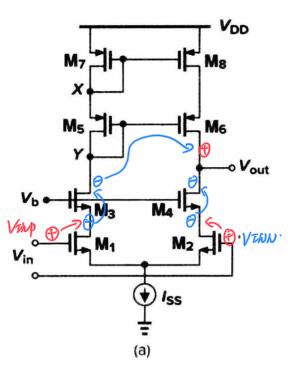
首先分析运放的右侧输入端。将左侧的输入端置零，并在右侧输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 M2，从 M2 的栅极传递到 M2 的漏极，极性反相，因此 M2 漏极处的极性为「㊀」；随后该极性经过晶体管 M4，从晶体管 M4 的源极传递到 M4 的漏极（即 Vout），极性同相，因此最终传递到输出时的极性为「㊀」。由此，该输入端为运放的负输入端。

随后对该运放的左侧输入端进行分析。将右侧的输入端置零，并在左侧输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 M1，从 M1 的栅极传递到 M1 的漏极，极性反相，因此 M1 漏极处的极性为「㊀」；随后该极性经过晶体管 M3，从晶体管 M3 的源极传递到 M3 的漏极（即 Y 点），极性同相，因此传递到 Y 点的极性为「㊀」；随后该信号又经过了晶体管 M6，从 M6 的栅极传递到 M6 的漏极（即 Vout），极性反相，因此最终传递到输出时的极性为「㊉」。由此，该输入端为运放的正输入端。

下图表示了该 Cascode 运放的两个输入端到输出端的极性传递过程。

3.3 折叠 Cascode 运放

折叠 Cascode 运放作为一种较为常用的电路结构，相比非折叠结构具有宽输入摆幅的优势；同时与非折叠结构相比，它的电路结构也较为复杂，从而使得输入端的正负判断起来更为复杂。这也使得很多新人在设计折叠共源共栅运放时，常常判断错该运放的正负输入端，进而导致电路的功能出现异常。

通常折叠式共源共栅运放具有两种常见的电路结构，分别为 NMOS 输入型和 PMOS 输入型。本篇博客将以 PMOS 输入型来举例，对该运放的极性传递特性进行分析。PMOS 输入的折叠 Cascode 运放的一种典型结构如下图所示。

该结构的运放同样可以使用极性传递法进行分析。这里同样首先分析运放的右侧输入端。将左侧的输入端置零，并在右侧输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 M2，从 M2 的栅极传递到 M2 的漏极，极性反相，因此 M2 漏极处的极性为「㊀」；随后该极性经过晶体管 M9，从晶体管 M9 的源极传递到 M9 的漏极（即 Vout），极性同相，因此最终传递到输出时的极性为「㊀」。由此，该输入端为运放的负输入端。

随后对该运放的左侧输入端进行分析。将右侧的输入端置零，并在左侧输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 M1，从 M1 的栅极传递到 M1 的漏极，极性反相，因此 M1 漏极处的极性为「㊀」；随后该极性经过晶体管 M8，从晶体管 M8 的源极传递到 M8 的漏极，极性同相，因此传递到 M8 的漏极的极性为「㊀」；随后该信号又经过了晶体管 M5，从 M5 的栅极传递到 M5 的漏极，极性反相，因此传递到 M5 的漏极的极性为「㊉」；最终，该极性经过晶体管 M7，从晶体管 M7 的源极传递到 M7 的漏极（即 Vout），极性同相，因此传递到输出端的极性为「㊉」。由此，该输入端为运放的正输入端。

下图表示了该折叠式 Cascode 运放的两个输入端到输出端的极性传递过程。

3.4 两级运放

对于两级运放，也可以使用同样的方式进行分析。通常两级运放可以看成是一个单极运放加上一个反相放大单元组成，因此，对于两级运放的正负输入端标注，可以直接把前面讲的单极运放的正负输入端反一下（即将原来的 VINP 改成 VINN，VINN 改成 VINP 即可），就标注好了。如果大家对这样标注不放心的话，也可以使用极性传递法来进行分析，这里本人也简单的举一个例子，如下图。

这里同样从运放的右侧输入端开始。将左侧的输入端置零，并在右侧输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 M2，从 M2 的栅极传递到 M2 的漏极，极性反相，因此 M2 漏极处的极性为「㊀」；随后该极性经过晶体管 M6，从晶体管 M6 的栅极传递到 M6 的漏极（即 Vout），极性反相，因此最终传递到输出时的极性为「㊉」。因此该输入端为运放的正输入端。

接下来分析左侧的输入端。将右侧的输入端置零，并在左侧输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 M1，从 M1 的栅极传递到 M1 的漏极，极性反相，因此 M1 漏极处的极性为「㊀」；随后该信号又经过了晶体管 M4，从 M4 的栅极传递到 M4 的漏极，极性反相，因此最终传递到 M4 漏极的极性为「㊉」。最后该信号经过了晶体管 M6，从 M6 的栅极传递到 M6 的漏极，极性反相，因此最终传递到输出漏极的极性为「㊀」。该输入端为运放的负输入端。

下图表示了该两级运放的两个输入端到输出端的极性传递过程。

4 全差分运放正负输入端分析

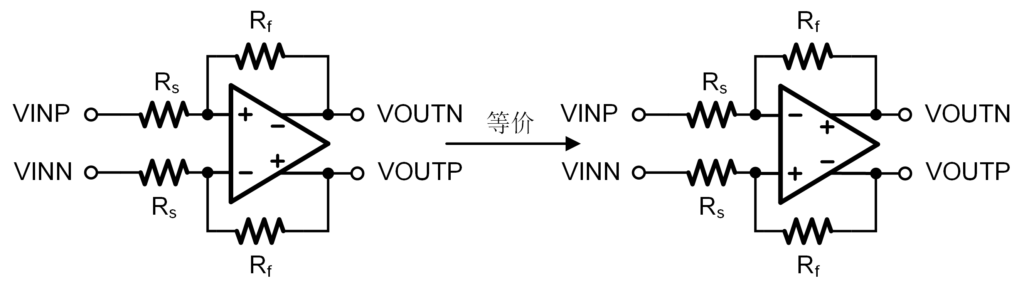
全差分运放的正负输入端的分析方法与单端运放一致，前面所描述的分析方法都可以应用到全差分运放的分析中去。但是与单端运放有所区别的是，由于全差分运放是完全对称的结构，因此它的正负输入端与正负输出端之间是「相对」的。所谓「相对」的意思是，如果将全差分运放的正输入端和负输入端进行对调，那么只需要将这个运放的正输出端和负输出端进行对调，这个运放在反馈环路中仍然能够正常工作，如下图。

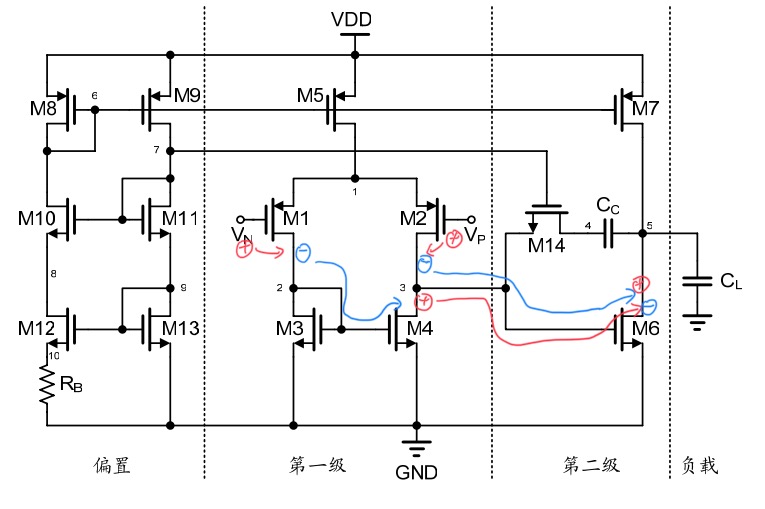
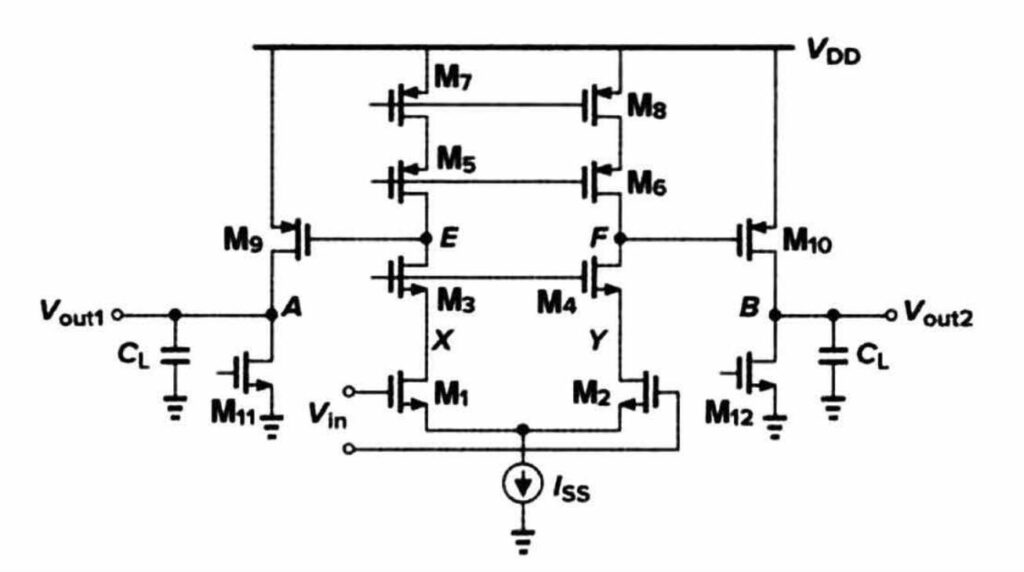
因此，在对全差分运放的正负输入端以及输入端进行判断时，可以采取「先指定好运放的正负输入端，随后在根据极性传递法则对运放的正负输出端进行判断」的方式，来判断运放的正负输出端，由此完成整个运放的正负输入和输出端的判断。这里本人使用下图所示的第一级为折叠式 Cascode 的两级运放来举例。

在分析全差分运放时，首先需要先指定好这个运放的正负输入端。这里指定运放的右侧输入端为同相（正）输入端 VINP，运放的左侧输入端为反相（负）输入端 VINN。随后就可以对运放的输出端的正负极性进行分析。在分析运放某个输出端的正负极性时，可以采用如下步骤进行：

首先在一个输入端施加一个极性为「㊉」的交流小信号，同时将另一个输入端置零，随后使用极性分析法分析与之对应的输出端的极性。如果该输出端的极性仍为「㊉」，则说明该输出端与输入端同相；如果该输出端极性为「㊀」，则说明该输出端与输入端反相。

随后就可以根据输入端的类型以及输入和输出端之间的正反相情况来判断该输出端的类型。如果输入端为正输入端，且输出和输入之间为同相，则该输出端也为正输出端，如果输出和输入之间为反相则为负输出端；如果输入端为负输入端，且输出和输入之间为同相，则该输出端也为负输出端，如果输出和输入之间为反相则为正输出端。（这部分可能有点绕，大家可能需要慢慢理解一下，总之就是先规定好输入，再根据输入和输出之间的关系，判定好输出端的正负）

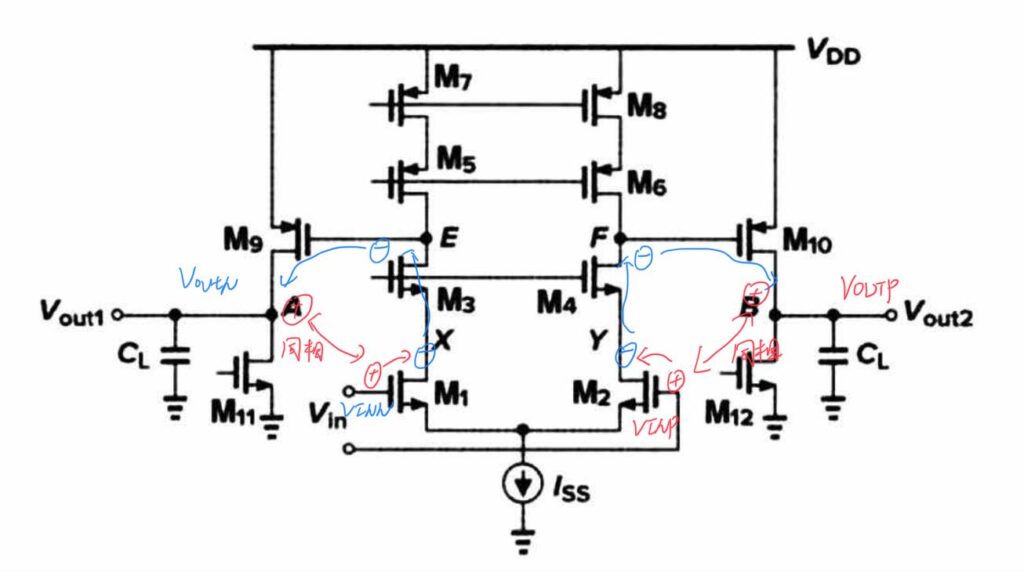
对于上图中的运放，右侧的输入端被规定为正输入端。分析时将左侧的输入端置零，并在右侧输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 M2，从 M2 的栅极传递到 M2 的漏极，极性反相，因此 M2 漏极处的极性为「㊀」；随后该信号经过晶体管 M4，从 M4 的源极传递到 M4 的漏极，极性同相，因此到 M4 漏极出的极性为「㊀」；最终该信号经过晶体管 M10，从 M10 的栅极传递到 M10 的漏极（即右侧输出端 Vout2），极性反相，因此右侧输出端的极性为「㊉」。通过上述分析可以看出，右侧输入出的极性为「㊉」，传递到右侧输出处的极性也为「㊉」，该输出端与输入端同相，由于输入端为 VINP，正输入端，那么输出端也为正输出端 VOUTP。

接下来分析左侧的输出端。分析时将右侧的输入端置零，并在左侧输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 M1，从 M1 的栅极传递到 M1 的漏极，极性反相，因此 M1 漏极处的极性为「㊀」；随后该信号经过晶体管 M3，从 M3 的源极传递到 M3 的漏极，极性同相，因此到 M3 漏极出的极性为「㊀」；最终该信号经过晶体管 M9，从 M9 的栅极传递到 M9 的漏极（即左侧输出端 Vout1），极性反相，因此左侧输出端的极性为「㊉」。因此，左侧输出端与左侧输入端同相，而左侧输入端为负输入端 VINN，则左侧输出端应为负输出端 VOUTN。至此，该运放的正负输入端和输出端判断完毕。

该全差分运放的具体的极性传递过程可以见下图。

5 一个稍微复杂的正负输入端分析问题举例

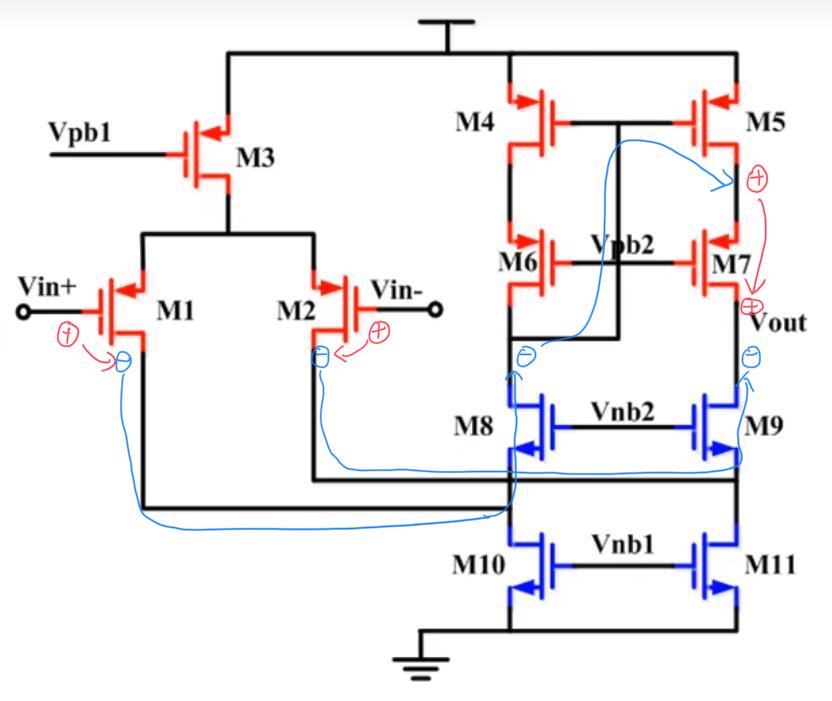
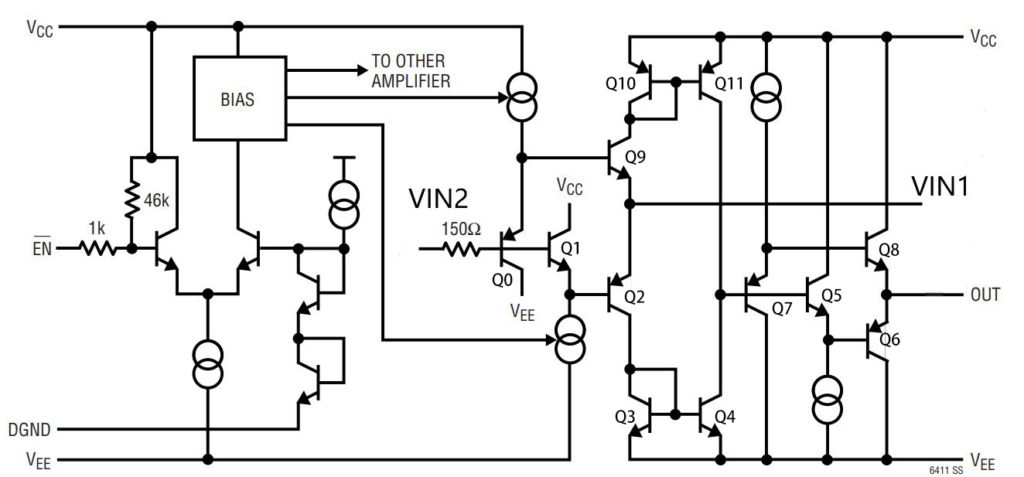
最后本文列举一个稍微复杂一些的运放结构，随后将使用上文的方法来判断该运放的正负输入端。该运放结构来自与产品 LT6411 的数据手册。本人对该结构图进行了一定的处理，隐去了其中的反馈环路部分以及运放的正负输入端标识，并对其中需要使用到的晶体管进行了一定的标注，最终结构如下图。

可以看出该运放为一个 BJT 结构的单极运放。对于 BJT 结构的运放，由于 BJT 的极性传递方式和 MOS 结构类似，因此该运放的分析过程也和之前 MOS 运放类似。

首先分析右侧的输入端 VIN1。将左侧的输入端 VIN2 置零，并在右侧 VIN1 输入端施加一个极性为「㊉」的交流小信号。该信号首先经过晶体管 Q2，从 Q2 的发射极传递到集电极，极性同相，因此 Q2 集电极处极性为「㊉」；随后该信号经过晶体管 Q4，从 Q4 的基极传递到 Q4 的集电极，极性反相，因此 Q4 集电极处极性为「㊀」；随后该信号又经过了晶体管 Q5 和 Q6，从 Q5 的基极传递到发射极，又从 Q6 的基极传递到发射极（即 OUT），这两个的极性都为同相传递，因此最终传递到输出的极性为「㊀」，因此 VIN1 为该运放的负输入端 VINN。

随后分析左侧的输入端 VIN2。将右侧的输入端 VIN1 置零，并在左侧 VIN2 输入端施加一个极性为「㊉」的交流小信号。该输入信号首先经过 Q1，从 Q1 的基极传递到发射极，极性为正，因此 Q1 发射极处的极性标识为「㊉」；随后该信号经过晶体管 Q2，从 Q2 的基极传递到集电极，极性反相，因此 Q2 集电极处极性为「㊀」；随后该信号又经过了晶体管 Q4，从 Q4 的基极传递到 Q4 的集电极，极性反相，因此 Q4 集电极处极性为「㊉」；随后该信号又经过了晶体管 Q5 和 Q6 到达输出端，这两步都为同相传递过程，因此最终信号到达输出端的极性为「㊉」，因此 VIN2 为该运放的正输入端 VINP。至此，运放的俩个输入端的正负判断完毕。

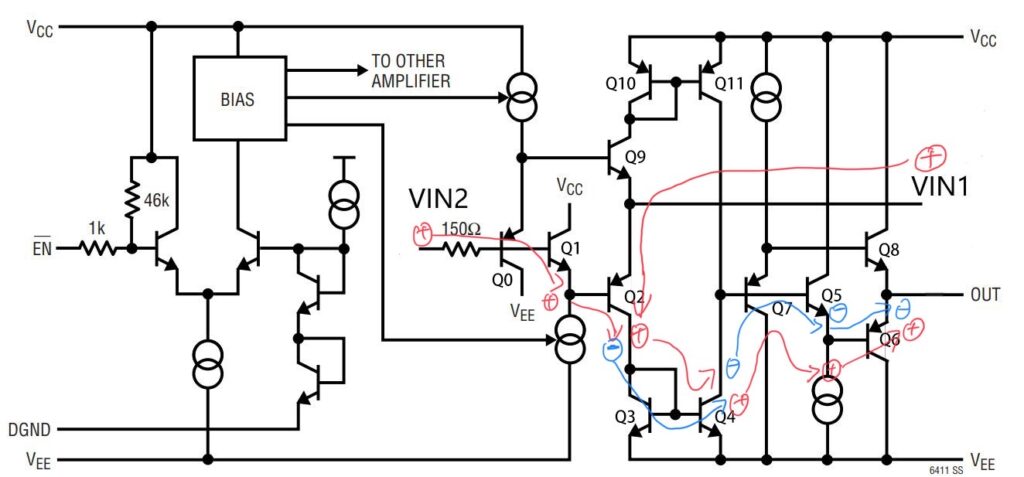
下图为 LT6411 数据手册中该运放的原图，通过该图可以看出上述的判断的输入端正负情况是正确的。

下图为该运放的极性传递过程分析图。

6 后记

对运放的正负输入端的判断是一个刚接触运放电路的新人非常容易出现问题的地方。大家后续如果遇到运放的正负输入端判定的问题时，可以尝试使用本篇教程中描述的极性传递的方法，来对该运放的正负输入端进行判别。该方法适用于绝大部分的运放结构（至少截至写完这篇教程这天我还没发现不适用的运放结构），大家可以放心的应用。