前言

最近在和同学们聊反馈时，不知怎么的就聊到了本科期间的模电课反馈的问题。这时本人突然想起，在本科的模电课上，杨老师曾经教过我们一种判断环路反馈极性的简单方法。在本人之后面对过的关于判断反馈环路的极性的问题中，这种方法屡试不爽，并且它可以毫无修改的应用在模拟集成电路中。

近日，本人又重新打开了《新概念模拟电路》这本书，并且重新回顾了一下这个方法——它被杨老师称为「环路极性法」。由于这种方法在判断反馈环路的极性时十分简洁好用，因此这里本人开了一篇文章，来介绍一下这种方法。

1 「环路极性法」的介绍

1.1 环路极性法的介绍

该方法可以在《新概念模拟电路》的 Section 59 中找到，这个方法的步骤为^[1]：

1. 首先找到感兴趣的反馈环路。
2. 在这个反馈环路中选择一个节点 A，一般可以选择放大器的输出节点
3. 假设在该节点 A 处存在一个正的变化量，并在节点上使用「㊉」符号表示该正变化量。
4. 顺着反馈环路，将这个变化量进行传递。在传递时，没经过一个关键的电路节点，就对该节点的变化量进行标注。正变化量用「㊉」符号表示，负变化量用「㊀」符号表示，如果没有变化就用「⓪」符号表示。
5. 当这个变化量再次传递到 A 节点时，此时表明该信号已经在反馈环路中传递一圈。如果最终传回的变化量为「㊉」即为正反馈，为「㊀」即为负反馈。

这种方法理解起来非常直观，同时操作起来也比较简单。通过对任一个环路使用这种方法，即可很容易的判断出环路反馈的极性正负。

1.2 一些典型的极性传递情况

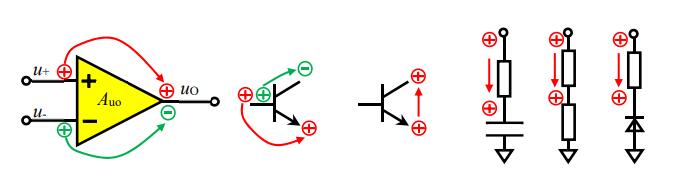
在《新概念模拟电路》的书中，杨老师已经给出了一些典型的极性传递情况，如下图所示：

通过这幅图可以看出：对于一个运放电路，它的极性传递情就是看运放的正负输入端即可。而对于一个 BJT 晶体管的极性传递来说，它只有从基极（B）到集电极（C）的极性传递为反相，而从基极（B）到发射极（E）和从发射级（E）到集电极（C）的极性传递方向都为同相。这种传递关系可以从典型的放大电路上来理解：输入在基极输出在集电极的共射级电路是反相放大的，而输入在基极输出在发射极的射极跟随器和输入在发射极输出在基极的共基极电路时是同相放大的。对于简单的阻容电路，只要把它们都看成是「阻抗」，在用简单的阻抗分压理论来理解，就可以很容易的理解这些极性传递情况。

而在现代的 CMOS 集成电路中，还有一些非常常用的器件书中并没有列出，例如 PNP 晶体管以及 NMOS 和 PMOS 晶体管等等。因此这里我也学着这本书绘图的方式，来列举一下这几个器件（为了方便，这里本人就选择手绘了）。

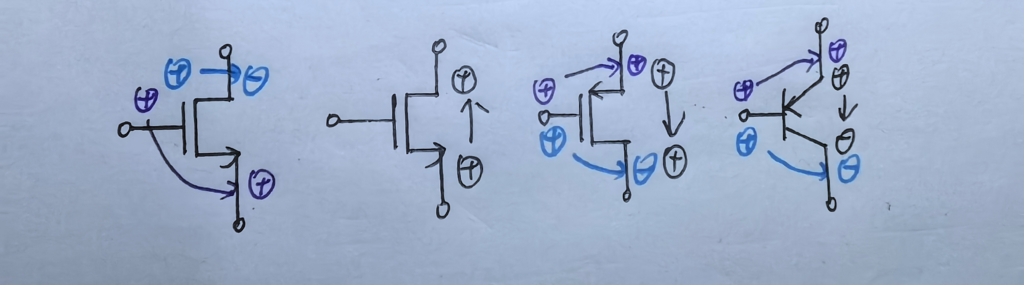
MOS 的极性传递方式同样可以从对应的放大器中来理解。共栅极放大器是反相放大的，所以从栅极（G）到漏极（D）就是反相传递的。而共栅极电路和源极跟随器电路都是同相放大的，因此从栅极（G）到源极（S）和从源极（S）到漏极（D）的极性传递方向都是相同的。

1.3 分立电路中的环路极性法示例

在杨建国老师的书的 Section 59 中，已经给出了很多极性传递的例子，基本上已经包含了各种情况。因此这里我就不班门弄斧了。大家如果想要更深入的了解环路极性法，可以去看一下这些示例。

2 集成电路中的环路极性法应用示例

对于集成电路，在遇到需要判断反馈环路极性的问题时，同样可以使用环路极性法来进行判断。这里本人将举几个例子，来说明在集成电路中如何使用环路极性法。

2.1 压控电流源电路

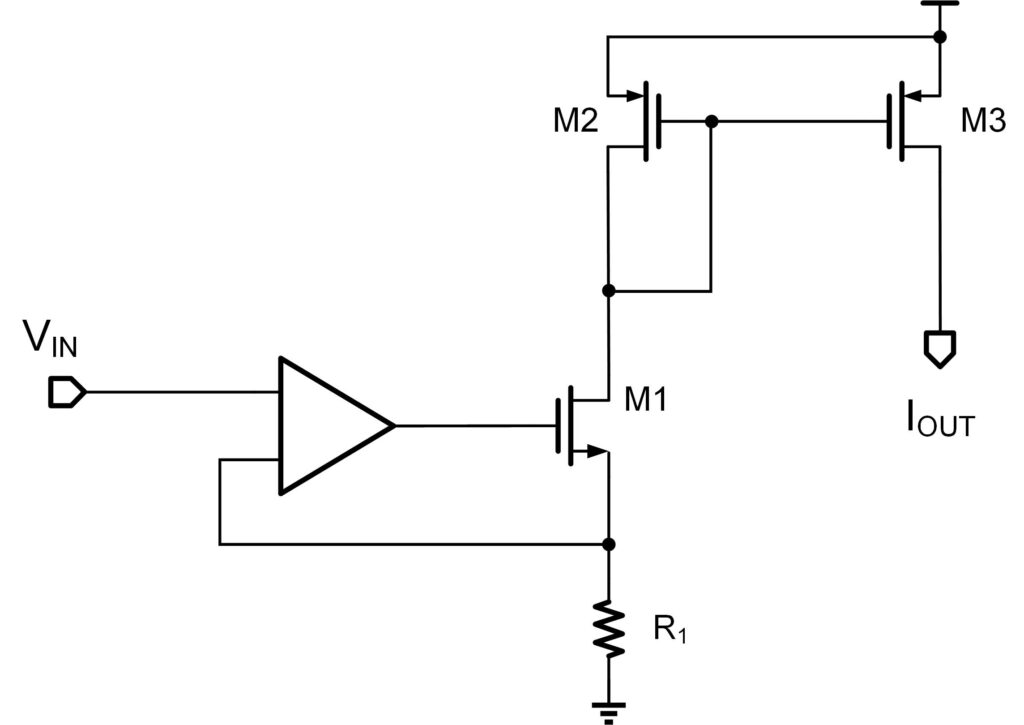
压控电流源电路，是一种非常经典的电流-电压反馈电路结构。它的基本结构如下图所示（这里先将运放的正负输入端标识隐去）：

对于该电路，如果想让其正常工作，一个重要的事情就是正确的连接运放的正负输入端。这时，就需要来分析反馈环路，判断出正负极性的传递情况，进而为运放的输入端填上正确的正负符号。

首先要做的是找到反馈环路。可以很明显的看出，这里有一个反馈环路，由 M1，R1 与运放共同组成。

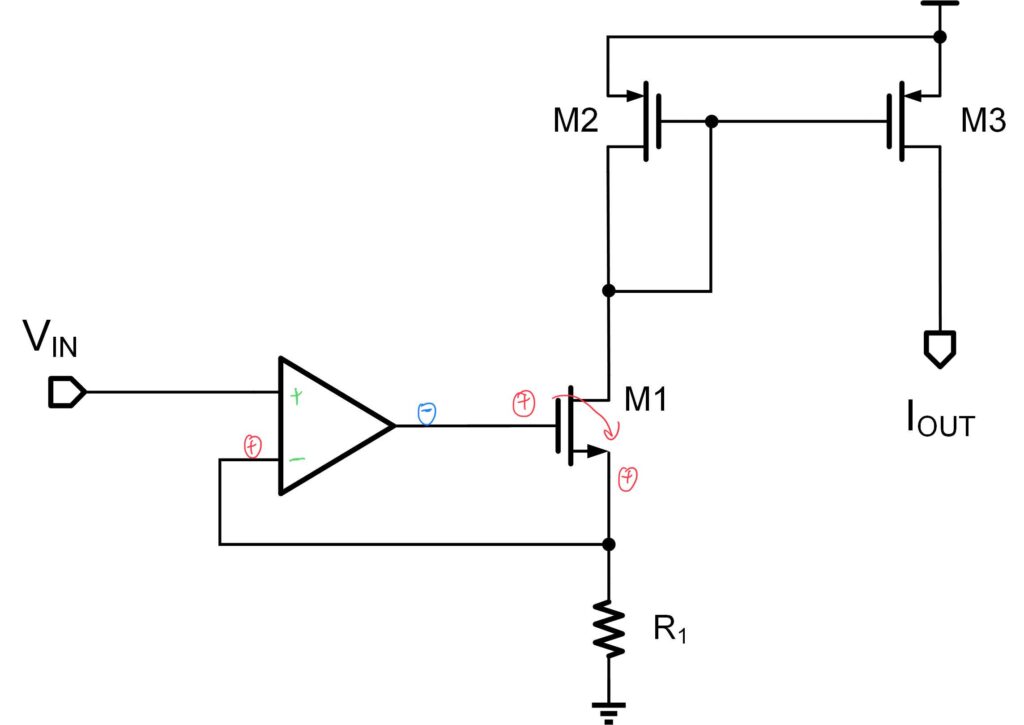
在判断信号的极性时，可以选择运放的输出端为起始点，并在信号起始点上标明一个「㊉」符号。该极性通过 MOS M1 来传递到 M1 的源端。这时由于栅极到源极的极性传递方向是同相的，因此 M1 的源端也可以标明一个「㊉」符号。而同时 M1 的源端也是该运放的一个输入端。

为了使得该运放正确的建立起负反馈，从该输入端到输出端的极性传递方向因该为反相。因此该输入端应为运放的负输入端。具体的分析过程如下图：

2.2 CMFB 电路

共模反馈电路是一种在模拟集成电路中应用的非常多的电路结构，它的主要作用是用来确定某些全差分结构的运放的输出共模电压。关于这些为什么需要共模反馈，大家可以去参考拉扎维的模拟 CMOS 集成电路书籍。这里我仅仅是举几个使用环路极性法判断共模反馈环路正负反馈的例子。

2.2.1 使用运放的共模反馈电路

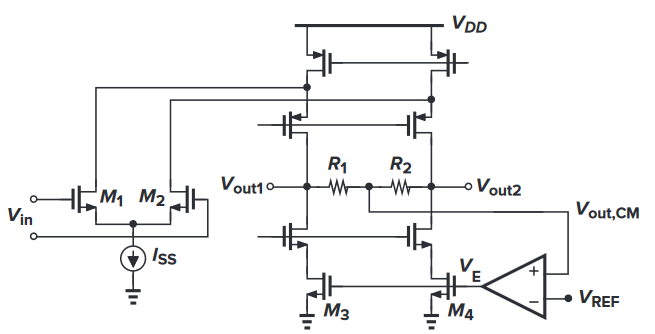
简单的使用两个电阻和一个运放，就可以完成一个共模反馈电路。一种使用这种结构的电路如下图所示（图源拉扎维的书中）：

对于该电路结构，要想共模反馈正常工作，同样需要对运放的正负输入端进行正确的连接。

从运放的输出端开始分析，最终可以得出该反馈环路的极性传递方式如下图所示。

这里需要注意的是，由于该电路为共模反馈电路结构，因此在使用环路极性法时，需要注意分析的应为共模信号在电路中的极性传递。而又由于从晶体管 M3、M4 到运放的共模输出端为一个共源共栅结构，为反相放大，因此电阻检测到的共模电压输出 $V_\mathrm{out,CM}$ 需要反馈回正输入端。

2.2.2 无运放的共模反馈电路

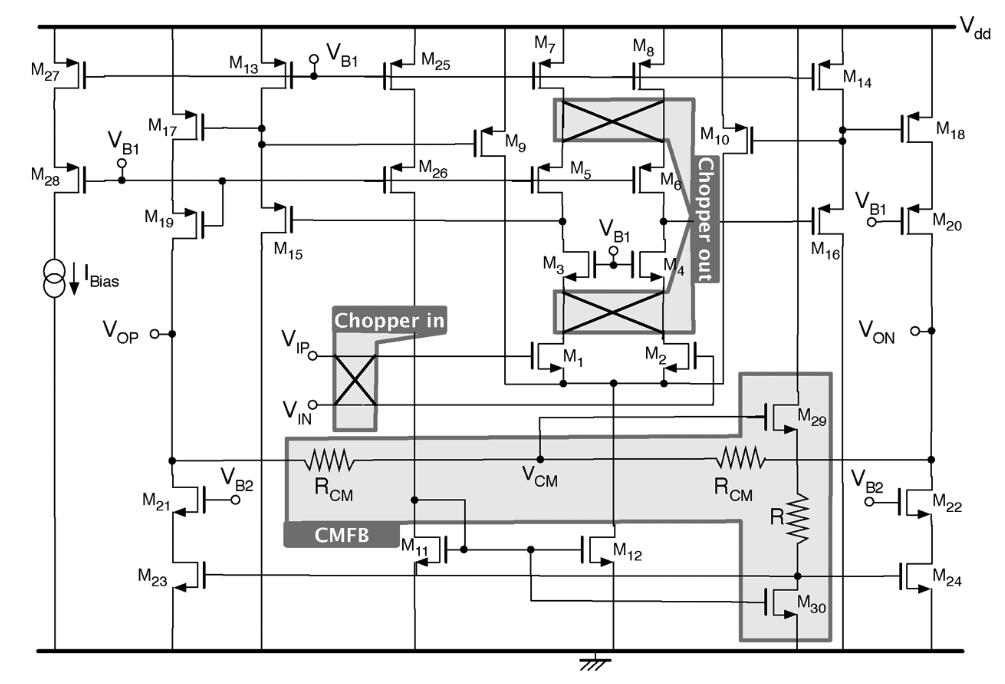
对于共模反馈电路，除了使用运放结构外，也可以使用一些其他的电路结构，来完成共模负反馈功能，例如下图中所示的电路^[2]：

该电路为一个全差分放大器结构。对于该放大器，目前先不关注其其他的电路结构，仅关注其输出级的共模反馈电路结构。该运放的输出级由 M17 – M24 组成，而共模反馈电路由 $R_\mathrm{CM}$、R、M20 和 M30组成。

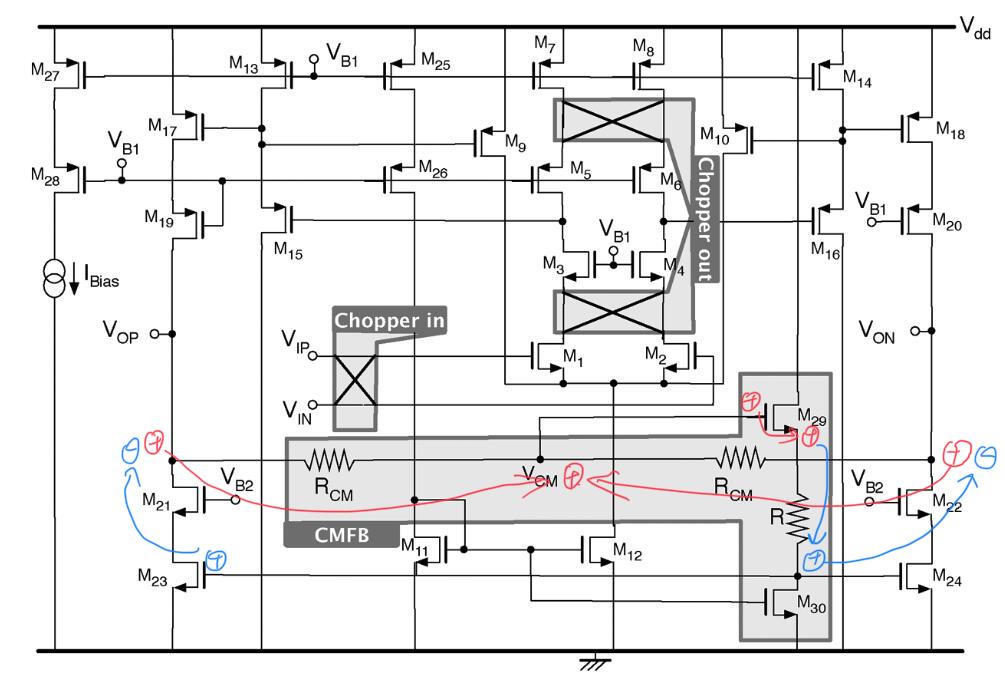
对于该反馈环路，同样可以使用环路极性的方式来进行分析，如下图。

其中，$R_\mathrm{CM}$ 用来获取共模电压 $V_\mathrm{CM}$，当运放输出的共模电压抬高时「㊉」，会导致 $V_\mathrm{CM}$ 抬高「㊉」，进而使得 M29 的栅极电压抬高「㊉」。而 M29 与电流源 MOS M30 和电阻 R 共同组成了一个源跟随器结构，因此 $V_\mathrm{CM}$ 抬高进而会导致 M24 和 M23 的栅极电压抬高「㊉」。而由于 M24 和 M23 与输出之间为一个共源共栅结构的放大器，因此使得运放输出的共模电压值下降「㊀」，完成共模负反馈。

2.2.3 其他常见的共模反馈电路

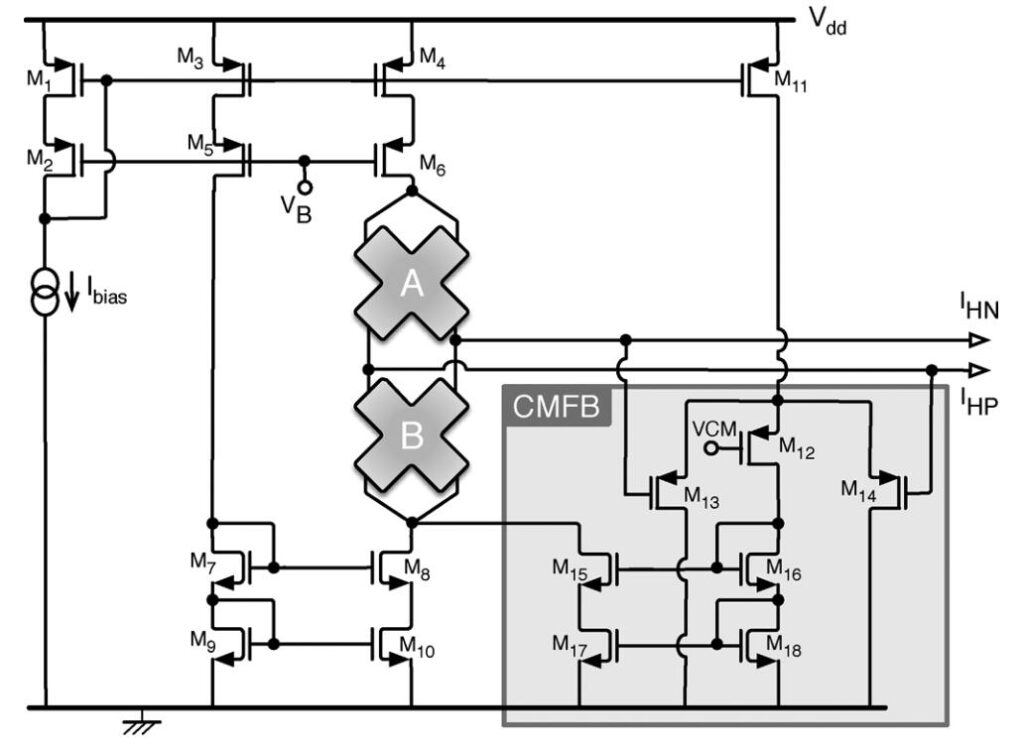
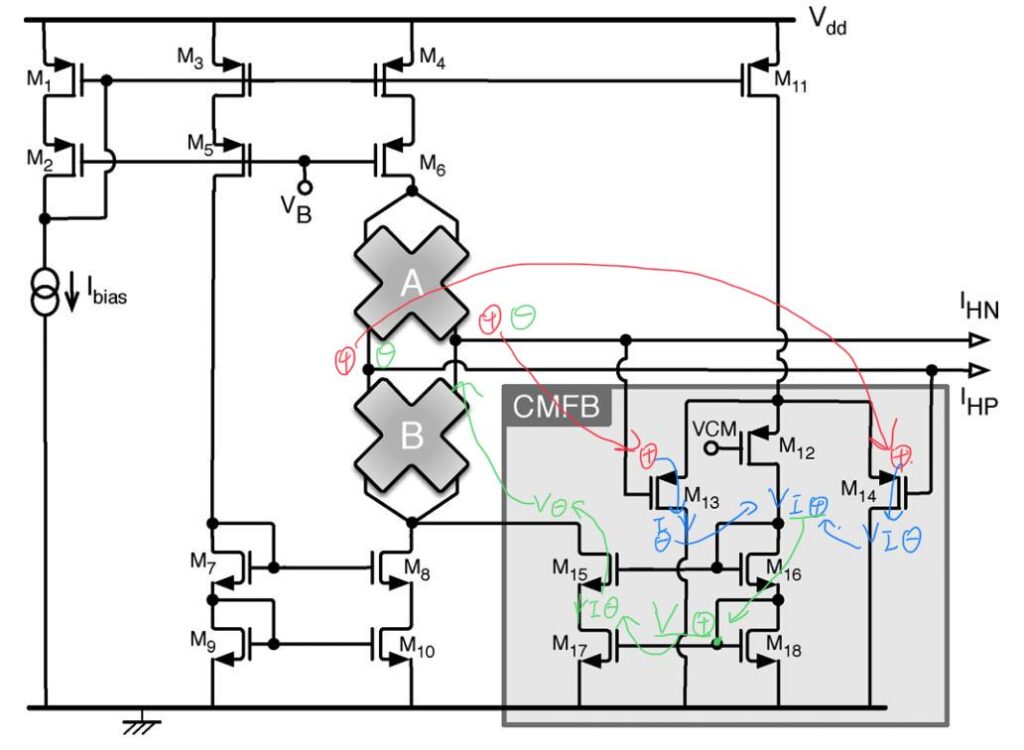
除了上面提到的共模反馈电路外，还有一些其他常见的共模反馈方式，如下图所示：

这个电路的反馈极性分析较为复杂。该电路中，A 和 B 为两个霍尔器件。这两个霍尔器件在一个电流的偏置作用下会产生一个输出电压。为了让该霍尔器件的输出更好的被后一级的系统处理，需要使得霍尔器件的输出具有一个确定的共模电平。因此这里使用了图中方框所示的电路来进行共模反馈。

该共模反馈电路的反馈极性同样可以使用环路极性法来分析，如下图。

当输出的共模电压升高时「电压 ㊉」，M13 与 M14 的栅极电压会抬升「电压 ㊉」，进而导致流过晶体管 M13 和 M14 的电流减少「电流 ㊀」。而 M11 为一个电流源管，它的存在使得流过 M12 – M14 晶体管的总电流和不变。因此这时 M13 和 M14 减少的电流将会进入到 M12 中去，进而使得 M16 和 M18 流过的电流增加「电流 ㊉」。由于电流镜的作用，这时流过 M15 和 M17 的电流也会增加「电流 ㊉」，分走了一部分电流源管 M4 与 M6 的电流，使得 M8 的栅极电压下降「电压 ㊀」，进而使得输出的共模电平下降「电压 ㊀」，完成负反馈。

2.3 带隙基准电路

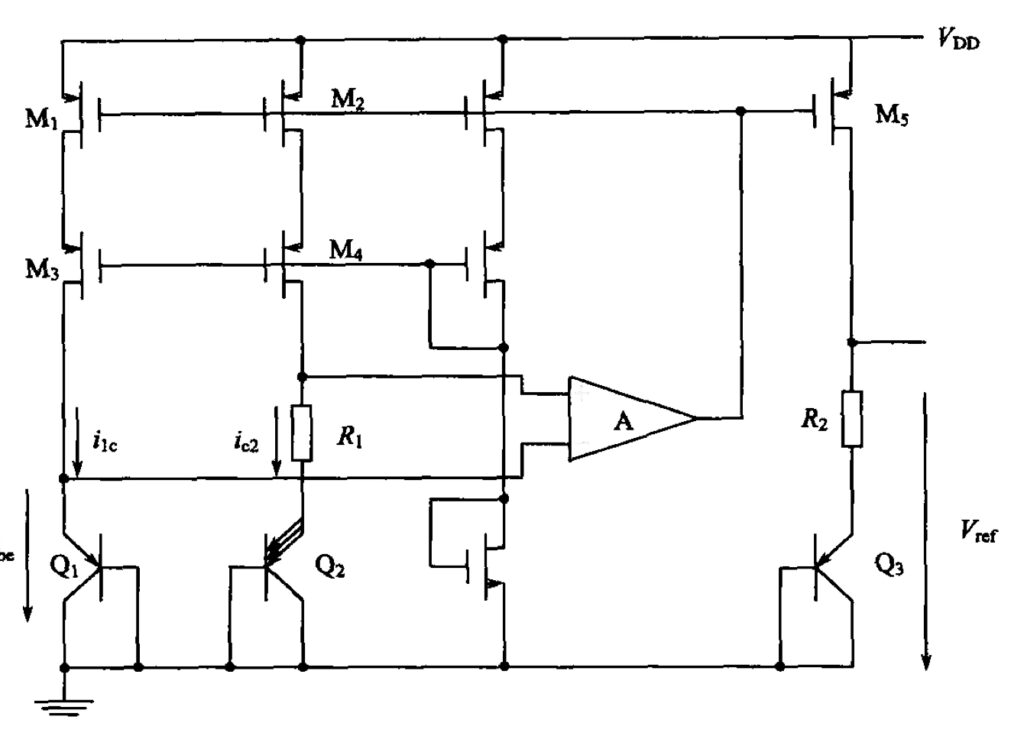
环路极性法也可以用来分析同时带有正负反馈的电路结构。使用运放的带隙基准电路也是一个很经典的同时带有正负反馈的电路。一种非常经典的带隙基准电路的结构如下图所示^[3]：

可以看出，这种结构的带隙基准电路中，会存在一个运放。既然存在一个运放，就一定会涉及到正负输入端的接法问题。只有正确的连接这个运放的正负输入端，这个电路才能正常的发挥功能。相信大家很多人再第一次设计这个电路的时候，都会把这个运放的正负输入端接反（别问我咋知道的，本人就这么干过），然后仿真发现电路完全不工作，并且电路的直流工作点非常的奇怪，运放的输出电压很高，这时候就要去考虑一下是不是运放的正负输入端接反了。

对于这个带隙基准电路，它的正负反馈情况以及输入端的放置方式也是同样可以通过环路极性法来分析的。

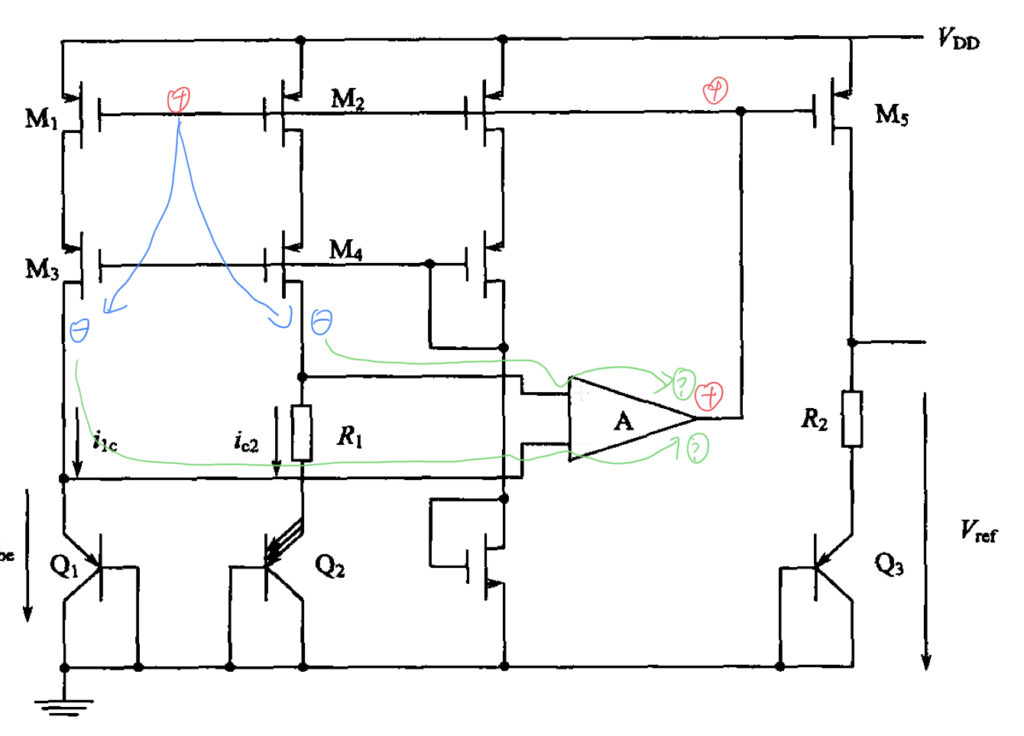
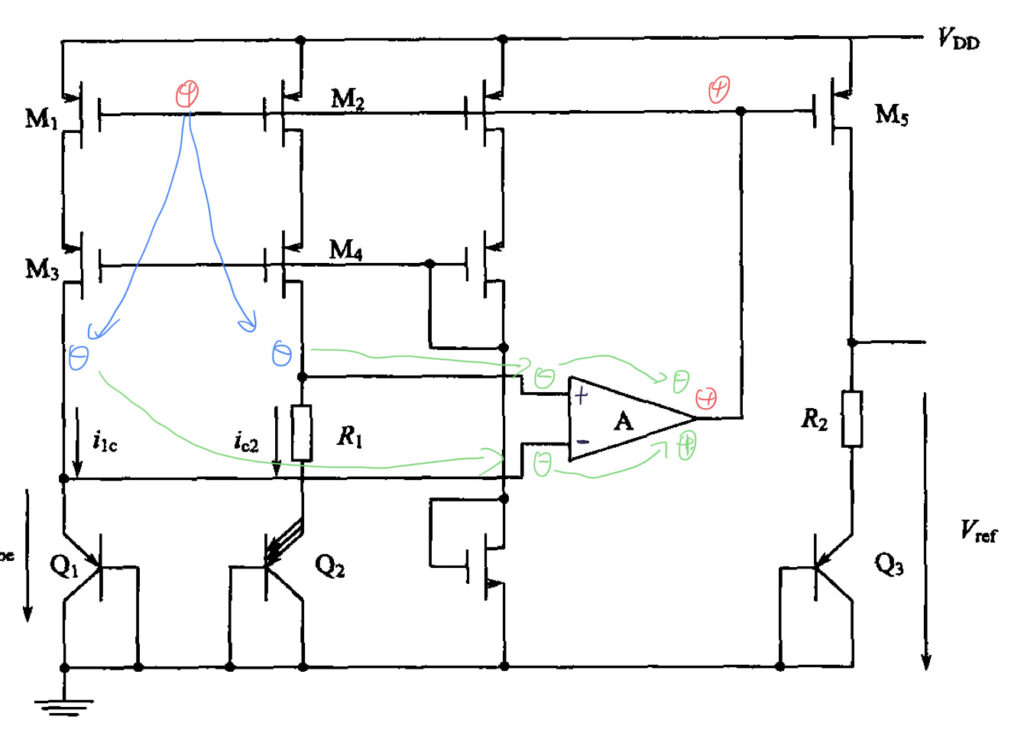
同样，我们可以从运放的输出端开始分析。假设运放的输出端的电压抬高「㊉」，该抬高的电压会传递到 M1 和 M2 的栅极上，这会使得 M1 和 M2 的栅极电压抬高「㊉」。而 M1 与 M3，M2 与 M4 组成的是一个 Cascode 共源极放大器结构，因此 M1 和 M2 的栅极到 M3 和 M4 的漏极的极性传递方向是反相的，因此因该在 M3 和 M4 的漏极上面标上一个「㊀」，如下图：

这时，问题就出现了——由于运放的作用，M3 和 M4 的漏极的极性会同时被传递到运放的输出端，并且传递的方向是一个同相一个反相；那么，该怎么设置运放的输入极性，最终系统才能完成一个负反馈呢？

可以看出，现在的问题关键在于，这个系统同时存在一个正反馈和一个负反馈，但是两者的反馈系数是不同的。如果相保证最后整个系统是处于一种负反馈的状态，那么就要保证运放正确的连接后，负反馈的反馈系数大于正反馈（也就是说负反馈强于正反馈），因此接下来需要对两条反馈环路的反馈系数进行分析：

在分析时，可以假设运放的输出有一个微小的电压变化 $\Delta v$，这个电压变化会传递到 M1 和 M2 的栅极，使得

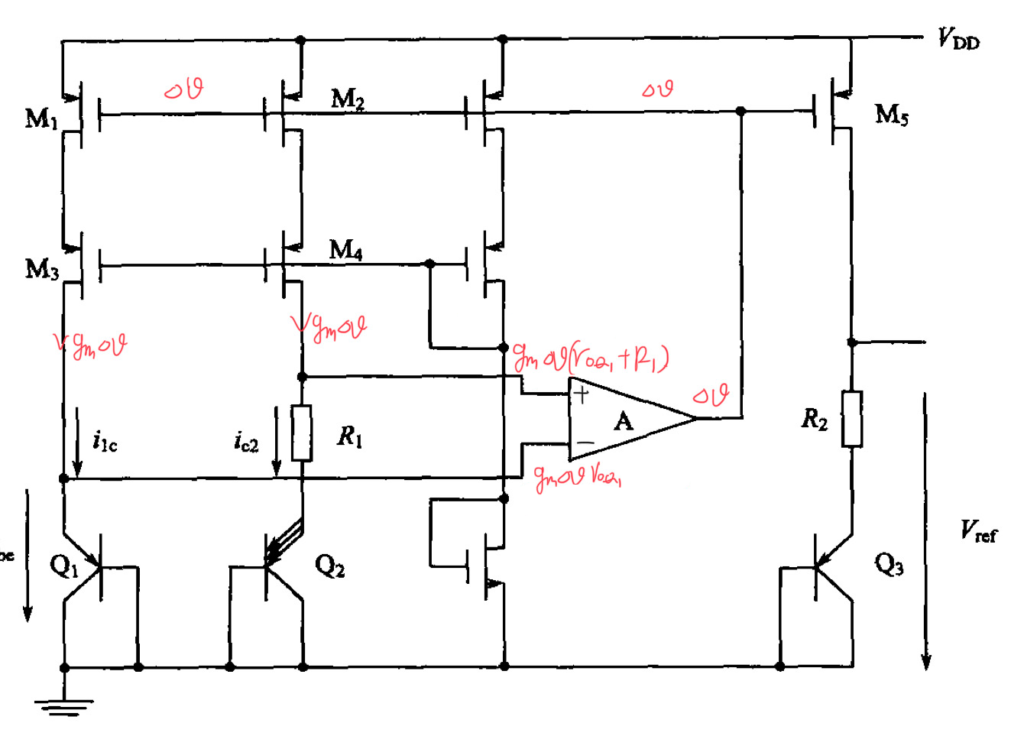
在分析时，可以假设运放的输出有一个微小的电压变化 $\Delta v$，这个电压变化会传递到 M1 和 M2 的栅极，使得 M1 和 M2 的栅极电压也变化一个 $\Delta v$。由于晶体管 M1 与 M2 的跨导的作用，Q1 和 Q2 两条支路里面的电流会变化一个 $g_m \Delta v$。而这个变化量作用在输出电阻上 ，就可以得到运放的输入端的电压变化量。对于 Q1 的支路来说，输出电阻可以近似等于晶体管 Q1 的输出电阻 $r_{oQ1}$，因此运放输入端的电压变化为 $g_m \Delta v r_{oQ1}$；而对于晶体管 Q2 所在的支路而言，输出电阻为晶体管 Q2 的输出电阻 $r_{oQ2}$ 和电阻 $R_1$ 的串联。因此运放另一个输入端的电压变化为 $g_m \Delta v （r_{oQ2} + R_1)$。而在带隙基准电路中，这两个晶体管的输出电阻通常差不多大，而一般 $R_1$ 会非常大。由此，可以很明显的得出：Q2 所在的支路的反馈能力更强，因此运放应使用正输入端与这条支路相连，这样就能确保最终的反馈为负反馈，如下图：

可以看出，通过使用环路极性法，再辅以一定的分析，就可以十分简单的判读出运放输入端的正确连接方式。

3 总结

在分立的模拟电路和模拟集成电路中，为了实现各种各样的需求，反馈结构具有非常多的应用。因此，学会如何使用一个简单好用的方式来判断电路的反馈极性还是非常重要的。杨建国老师的「环路极性法」一种本人觉得不管是在分立模拟电路还是集成电路中都比较简洁好用的分析方式，并且适用范围较广，大家可以去了解一下。如果文章中还有什么问题，也请大家批评指正。